Material for speakers: Difference between revisions
Jump to navigation
Jump to search
Vincenzo Cirigliano, Ryuichiro Kitano, Yasuhiro Okada, and Paula Tuzon, Phys. Rev. D 80, 013002 (2009)
PIP-II public web site
E. Pozdeyev, Rare Processes and Precision Frontier Town Hall (2020)
[3] "Pion-production target design for Mu2e-II: status update" 1st Muon Community Meeting (2021)
[4] "Early considerations for muon collider targetry at CERN"
"Design and studies for the Mu2e-II tracker", DPF 2021 [5]
COMET tracker (2020 NIM) [6]
COMET tracker (2016 slides) [7]
[8] "A Novel Scintillator Detector for the Mu2e-II Experiment and a Muon Tomography Probe of the Interior of the Great Pyramid"
[9] Muon-ion collider for BNL (2021)
[10] Mu2e-II Snowmass 22 Letter of Interest (2020)
[11] 1st muon community meeting (CERN), 20-21 May 2020
[12] Mu2e-II theory Snowmass 22 Letter of Interest (2020)
[13] COMET Phase-I TDR (2020)
[14] Muon colliders (2019)
[15] Mu2e-II Expression of Interest (2018)
| Line 63: | Line 63: | ||
values of <math>R_{\mu e}</math> indicated in the legends. | values of <math>R_{\mu e}</math> indicated in the legends. | ||
In more detail: (left) Simulation of the energy distributions of electrons from conversion and the high energy tail of DIO's, for Mu2e. The assumption is <math>6.7\times 10^{17}</math> stopped muons and a conversion electron (CE) rate of <math>1\times10^{-16}</math>. The electron energies are broadened by energy straggling in the stopping target and the Inner Proton Absorber, and by energy straggling and multiple scattering in the Tracker; | In more detail: (left) Simulation of the energy distributions of electrons from conversion and the high energy tail of DIO's, for Mu2e. The assumption is <math>6.7\times 10^{17}</math> stopped muons and a conversion electron (CE) rate of <math>1\times10^{-16}</math>. The electron energies are broadened by energy straggling in the stopping target and the Inner Proton Absorber, and by energy straggling and multiple scattering in the Tracker; | ||
(center) Simulation of the energy distributions of electrons from conversion and the high energy tail of DIO's, for Mu2e-II. The assumption is <math>1\times10^{19}</math> stopped muons and a CE rate of <math>1\times10^{-17}</math | (center) Simulation of the energy distributions of electrons from conversion and the high energy tail of DIO's, for Mu2e-II. The assumption is <math>1\times10^{19}</math> stopped muons and a CE rate of <math>1\times10^{-17}</math>. The energy resolution is assumed to be the same as that expected for Mu2e. There is now a substantial overlap between the DIO background and the CE signal; | ||
(right) Simulation of the energy distributions of electrons from conversion and the high energy tail of DIO's, for Mu2e-II. The assumption is <math>1\times10^{19}</math> stopped muons and a CE rate of <math>1\times10^{-17}</math | (right) Simulation of the energy distributions of electrons from conversion and the high energy tail of DIO's, for Mu2e-II. The assumption is <math>1\times10^{19}</math> stopped muons and a CE rate of <math>1\times10^{-17}</math>. The energy resolution is assumed to be the two times better than Mu2e (a goal of Mu2e-II). | ||
There is now much less overlap between the DIO background and the CE signal, compared to the center plot. | There is now much less overlap between the DIO background and the CE signal, compared to the center plot. | ||
]] </li> | ]] </li> | ||
Revision as of 15:51, 28 July 2021
Mu2e
Mu2e public results and material for speakers
Theory
-
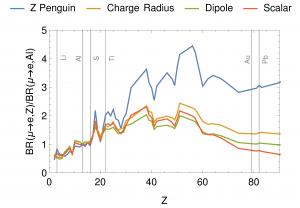 Z dependence of µ → e conversion rates for some sample scenarios [1].
Z dependence of µ → e conversion rates for some sample scenarios [1]. -
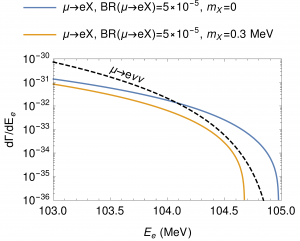 Tail of the electron spectrum for DIOs and for two [math]\displaystyle{ \mu\to eX }[/math] scenarios [2].
Tail of the electron spectrum for DIOs and for two [math]\displaystyle{ \mu\to eX }[/math] scenarios [2].
References
PIP-II accelerator
Beamline
Production target
Production solenoid
Tracking
-
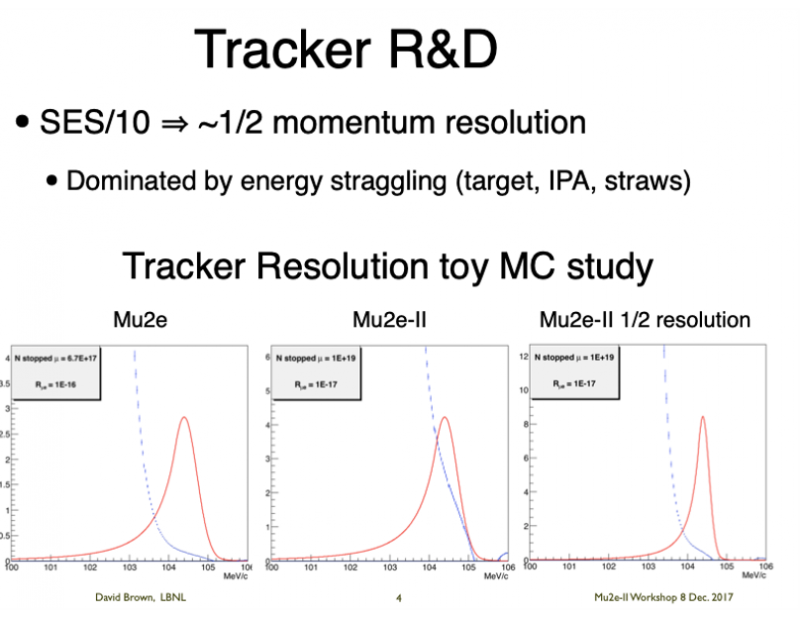 Slide illustrating the requirement on track resolution for Mu2e-II compared with Mu2e. Note that the resolution has contributions from several sources - the tacker itself, absorber material, and target material. The blue dashed curve on each plot indicates the electron spectrum from muon decays in orbit (DIOs). The red curves show the conversion electron spectrum for the values of [math]\displaystyle{ R_{\mu e} }[/math] indicated in the legends. In more detail: (left) Simulation of the energy distributions of electrons from conversion and the high energy tail of DIO's, for Mu2e. The assumption is [math]\displaystyle{ 6.7\times 10^{17} }[/math] stopped muons and a conversion electron (CE) rate of [math]\displaystyle{ 1\times10^{-16} }[/math]. The electron energies are broadened by energy straggling in the stopping target and the Inner Proton Absorber, and by energy straggling and multiple scattering in the Tracker; (center) Simulation of the energy distributions of electrons from conversion and the high energy tail of DIO's, for Mu2e-II. The assumption is [math]\displaystyle{ 1\times10^{19} }[/math] stopped muons and a CE rate of [math]\displaystyle{ 1\times10^{-17} }[/math]. The energy resolution is assumed to be the same as that expected for Mu2e. There is now a substantial overlap between the DIO background and the CE signal; (right) Simulation of the energy distributions of electrons from conversion and the high energy tail of DIO's, for Mu2e-II. The assumption is [math]\displaystyle{ 1\times10^{19} }[/math] stopped muons and a CE rate of [math]\displaystyle{ 1\times10^{-17} }[/math]. The energy resolution is assumed to be the two times better than Mu2e (a goal of Mu2e-II). There is now much less overlap between the DIO background and the CE signal, compared to the center plot.
Slide illustrating the requirement on track resolution for Mu2e-II compared with Mu2e. Note that the resolution has contributions from several sources - the tacker itself, absorber material, and target material. The blue dashed curve on each plot indicates the electron spectrum from muon decays in orbit (DIOs). The red curves show the conversion electron spectrum for the values of [math]\displaystyle{ R_{\mu e} }[/math] indicated in the legends. In more detail: (left) Simulation of the energy distributions of electrons from conversion and the high energy tail of DIO's, for Mu2e. The assumption is [math]\displaystyle{ 6.7\times 10^{17} }[/math] stopped muons and a conversion electron (CE) rate of [math]\displaystyle{ 1\times10^{-16} }[/math]. The electron energies are broadened by energy straggling in the stopping target and the Inner Proton Absorber, and by energy straggling and multiple scattering in the Tracker; (center) Simulation of the energy distributions of electrons from conversion and the high energy tail of DIO's, for Mu2e-II. The assumption is [math]\displaystyle{ 1\times10^{19} }[/math] stopped muons and a CE rate of [math]\displaystyle{ 1\times10^{-17} }[/math]. The energy resolution is assumed to be the same as that expected for Mu2e. There is now a substantial overlap between the DIO background and the CE signal; (right) Simulation of the energy distributions of electrons from conversion and the high energy tail of DIO's, for Mu2e-II. The assumption is [math]\displaystyle{ 1\times10^{19} }[/math] stopped muons and a CE rate of [math]\displaystyle{ 1\times10^{-17} }[/math]. The energy resolution is assumed to be the two times better than Mu2e (a goal of Mu2e-II). There is now much less overlap between the DIO background and the CE signal, compared to the center plot.
References
Calorimeter
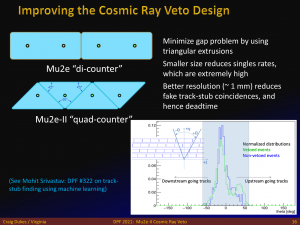
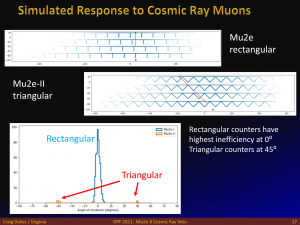
Cosmic Ray Veto
The Mu2e-II Cosmic Ray Veto will need to cope with roughly a factor 3 higher instantaneous rates from accelerator compared with Mu2e as well as a factor of three higher live time (i.e., cosmic rays), because of the higher duty factor for Mu2e-II compared with Mu2e.